
Hàm số lượng giác là một phần quan trọng của chương trình học toán và khoa học tự nhiên. Ngoài việc giúp học sinh hiểu rõ hơn về các khái niệm cơ bản trong hình học và tính toán, như độ dài các cạnh, góc và phương trình, các hàm số lượng giác còn hữu ích trong việc giải quyết các vấn đề thực tế, như trong lĩnh vực địa chất, thiết kế xây dựng, máy tính và nhiều lĩnh vực khác. Vì vậy, học sinh cần phải nắm vững kiến thức về hàm số lượng giác để có thể áp dụng vào thực tiễn.
Bài viết dưới đây thuthuatpc.vn sẽ tổng hợp cho các bạn chi tiết các công thức bảng giá trị lượng giác đặc biệt đầy đủ và cần thiết.
Công thức lượng giác cơ bản

- Thơ nhớ công thức lượng giác cơ bản
Bắt được quả tang
Sin nằm trên cos
Côtang cãi lại
Cos nằm trên sin!
Công thức cộng lượng giác

- Thơ nhớ công thức cộng lượng giác
Cos cộng cos thì bằng hai cos cos
Cos trừ cos phải bằng trừ hai sin sin
Sin cộng sin thì bằng hai sin cos
Sin trừ sin bằng hai cos sin.
Sin thì sin cos cos sin
Cos thì cos cos sin sin nhớ nha dấu trừ
Tan tổng thì lấy tổng tan
Chia một trừ với tích tan, dễ òm.
Công thức nhân
- Công thức nhân đôi
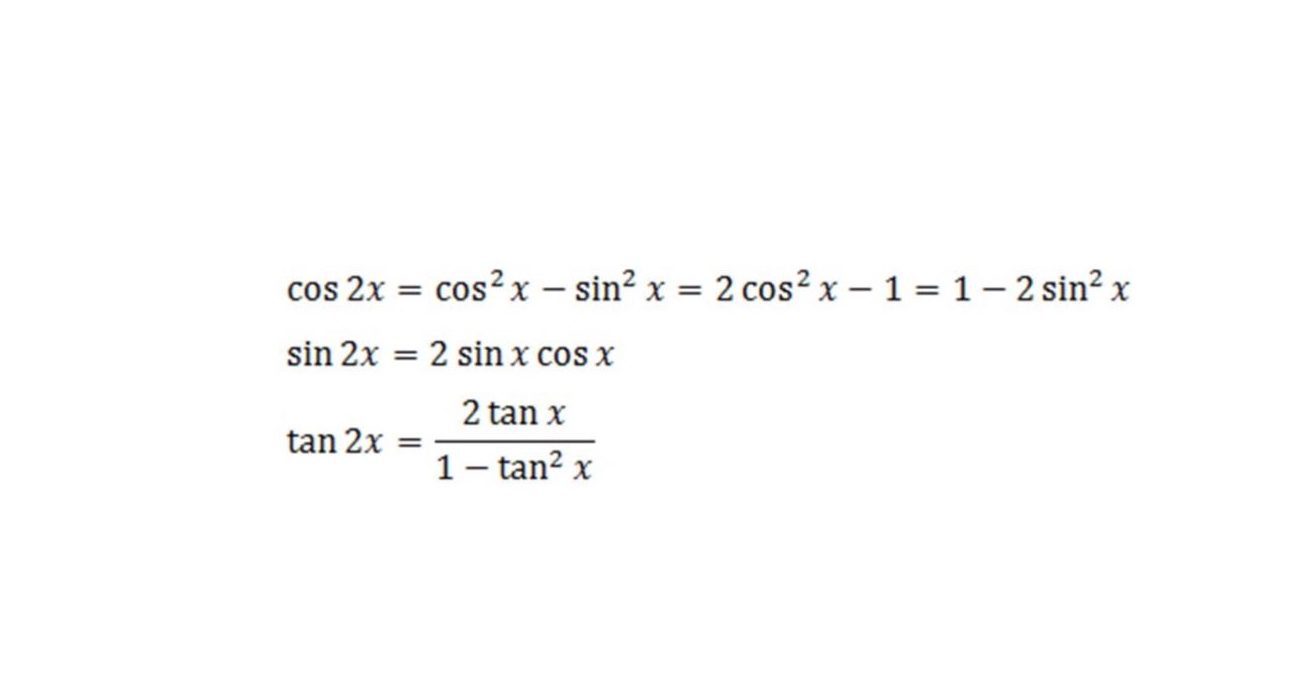
- Công thức nhân ba

- Sin 3x = 3 Sin x – 4 Sin3 x
Cos 3x = 4 Cos2 x – 3 Cos x
- Thơ nhớ công thức nhân 3
Nhân ba một góc bất kỳ, sin thì ba bốn, cos thì bốn ba, dấu trừ đặt giữa hai ta, lập phương chỗ bốn,… thế là ok.
- Công thức nhân bốn

Xem thêm>>[#1] Bảng đo độ dài và đo khối lượng chính xác, dễ học thuộc nhất
Công thức biến tổng thành tích

Thớ nhớ công thức biến tổng thành tích
sin tổng lập tổng sin cô
cô tổng lập hiệu đôi cô đôi chàng
còn tan tử cộng đôi tan (hoặc là: tan tổng lập tổng hai tan)
một trừ tan tích mẫu mang thương sầu
gặp hiệu ta chớ lo âu,
đổi trừ thành cộng ghi sâu vào lòng
Công thức biến tích thành tổng

Thơ nhớ công thức biến tích thành tổng
Cos cos nửa cos-cộng, cộng cos-trừ
Sin sin nửa cos-trừ trừ cos-cộng
Sin cos nửa sin-cộng cộng sin-trừ
Công thức hạ bậc

Nghiệm của phương trình lượng giác

Công thức các cung liên kết trên đường tròn lượng giác
Mẹo nhớ: cos đối, sin bù, phụ chéo, tan hơn kém π
Hai góc đối nhau:
cos (-x) = cos x
sin (-x) = -sin x
tan (-x) = -tan x
cot (-x) = -cot x
Hai góc bù nhau:
sin (π – x) = sin x
cos (π – x) = -cos x
tan (π – x) = -tan x
cot (π – x) = -cot x
Xem ngay>> [Toán học] Công Thức Cách Tính Chiều Dài Hình Chữ Nhật Và Ví Dụ Có Lời Giải
Hai góc phụ nhau:
sin (π/2 – x) = cos x
cos (π/2 – x) = sin x
tan (π/2 – x) = cot x
cot (π/2 – x) = tan x
Hai góc hơn kém π:
sin (π + x) = -sin x
cos (π + x) = -cos x
tan (π + x) = tan x
cot (π + x) = cot x
Hai góc hơn kém π/2:
sin (π/2 + x) = cos x
cos (π/2 + x) = -sin x
tan (π/2 + x) = -cot x
cot (π/2 + x) = -tan x
Bảng giá trị lượng giác một số góc đặc biệt

Công thức tổng và hiệu của sin x và cos x
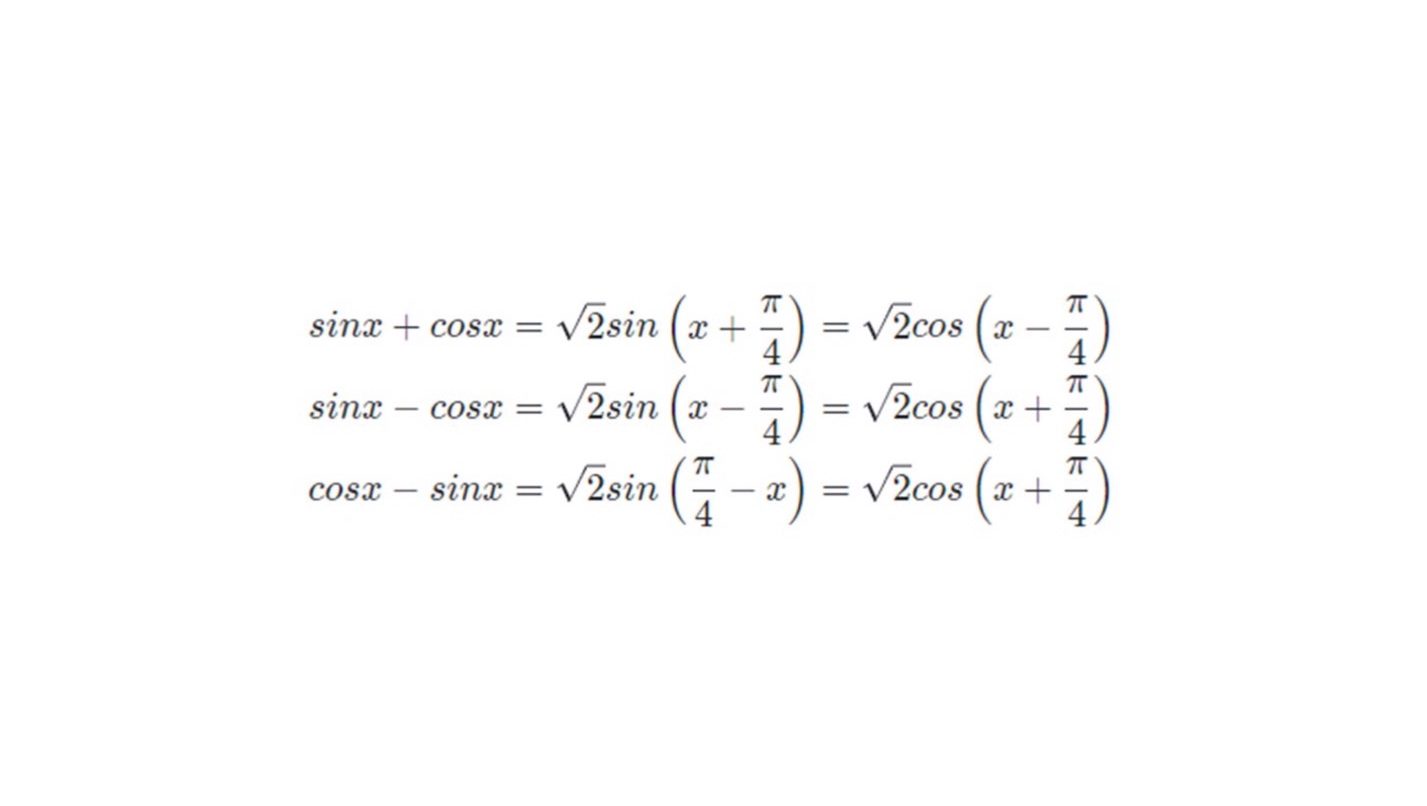
Công thức chia đôi

Công thức kết hợp với hằng đẳng thức đại số
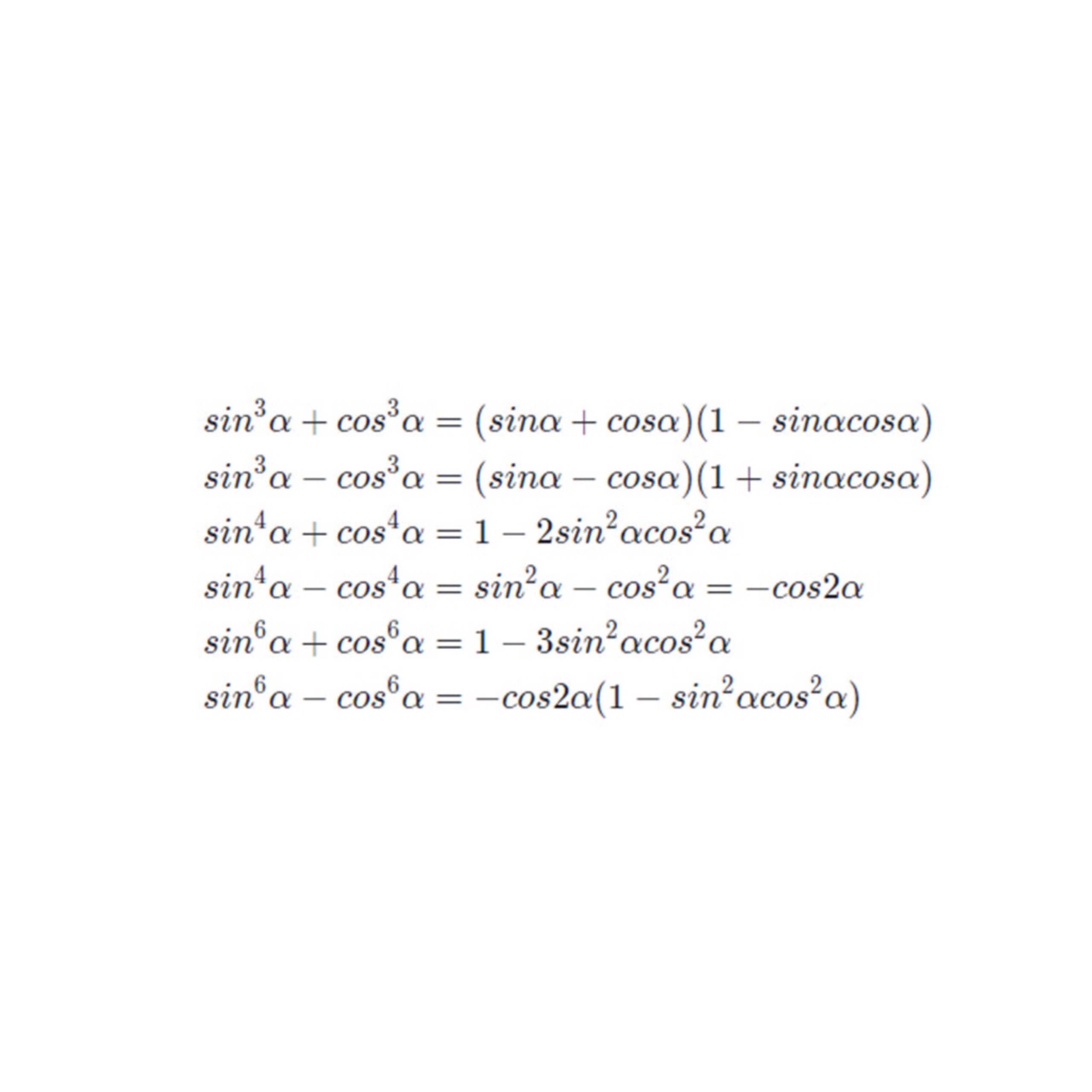
Xem thêm>>[Share] Thế Nào Là Số Nguyên Tố? Ví Dụ Minh Hoạ, Tính Chất, Bảng Số Nguyên Tố
Nguồn gốc của các công thức lượng giác
Đầu tiên chúng ta hãy tìm hiểu về nguồn gốc của lượng giác. Nguồn gốc của lượng giác có thể bắt nguồn từ người Ai Cập cổ đại, người Babylon và Nền văn minh Thung lũng Indus cổ đại có niên đại 3000 năm. Các nhà toán học Ấn Độ cổ đại đã đi tiên phong trong việc giải tích các đại số chưa biết để sử dụng trong các phép tính thiên văn bằng lượng giác. Các nhà toán học Ấn Độ đã phát triển các công thức lượng giác và sử dụng chúng để giải quyết các vấn đề liên quan đến thiên văn học và địa lý. Nhà toán học Lakatha là nhà toán học duy nhất được biết đến ngày nay đã sử dụng hình học và lượng giác trong tính toán thiên văn trong cuốn sách Vedanga Jyotisha của ông, hầu hết các tác phẩm của ông đã bị phá hủy khi Ấn Độ bị người nước ngoài xâm chiếm.
Khoảng năm 150 trước Công nguyên, nhà toán học Hy Lạp Hipparchus đã biên soạn một bảng lượng giác để giải các hình tam giác.
Một nhà toán học Hy Lạp khác, Ptolemy đã phát triển thêm các phép tính lượng giác vào khoảng năm 100 sau Công nguyên.
Nhà toán học Silesian Bartholomew Pytiscus đã xuất bản công trình có ảnh hưởng của ông về lượng giác vào năm 1595 và giới thiệu thuật ngữ này sang tiếng Anh và tiếng Pháp.
Xem thêm>>[Share] 1 Giây Bằng Bao Nhiêu Tích Tắc(Mili Giây)?1 Giờ Bằng Bao Nhiêu Tích Tắc???
Trên đây là các công thức và bảng giá trị lượng giác đặc biệt quan trọng mà các bạn học sinh cần phải nhớ. Hi vọng bài viết thuthuatpc.vn đã cung cấp cho các bạn các thông tin hữu ích. Cảm ơn các bạn đã theo dõi.
