
Hình thoi là một trong những hình rất cơ bản và được phổ biến rất nhiều trong chương trình học và trong cuộc sống. Bài viết dưới đây thuthuatpc.vn sẽ cung cấp một số công thức để tính chu vi và diện tích hình thoi, bài tập liên quan cụ thể như sau.
Hình thoi là gì?

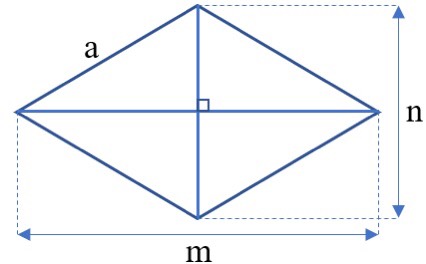
Hình thoi là tứ giác có bốn cạnh bằng nhau hay là hình bình hành có hai đường chéo vuông góc bằng nhau, có hai cạnh bên bằng nhau có hai đường chéo vuông góc với nhau và vắt nhau tại trung điểm mỗi đường đồng thời là đường phân giác của mỗi góc.
Trong trường hợp hình thoi có bốn góc vuông trong bằng nhau thì hình thoi được xác định là hình vuông như vậy hình vuông là một trường hợp đặc biệt của hình thoi vì nó có bốn cạnh dài bằng nhau và có bốn góc vuông. Tất cả các hình vuông đều là hình thoi nhưng không phải mọi hình thoi đều là hình vuông.
Xem thêm>>[Toán Học] Công Thức Diện Tích, Phương Trình Chính Tắc Hình Elip
Tính chất của hình thoi
Thứ nhất hình thoi đầy đủ tính chất của hình bình hành: cạnh đối song song với nhau và bằng nhau, các góc đối bằng nhau hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Thứ 2, hình thoi có các góc đối nhau bằng nhau tổng các góc trong hình thoi bằng 360 độ
Thứ 3, hình thoi có hai đường chéo vuông góc và cắt nhau tại trung điểm của mỗi đường
Thứ tư hình thoi có hai đường chéo là đường phân giác của các góc trong hình thoi.
Dấu hiệu nhận biết của hình thoi

Dấu hiệu 1: Hình thoi là tứ giác có 4 cạnh bằng nhau
Dấu hiệu 2: Hình thoi là tứ giác có hai đường chéo vuông góc với nhau tai trung điểm của mỗi đường hình thoi
Dấu hiệu 3: Hình thoi là hình bình hành có hai cạnh kề bằng nhau
Dấu hiệu 4: Hình thoi là hình bình hành có hai đường chéo vuông góc với nhau.
Dấu hiệu 5: hình thoi là hình bình hành có đường chéo là đường phân giác của mỗi góc.
Xem thêm>>[Toán Học] Công Thức, Bài Tập Tính Chu Vi, Diện Tích Của Hình Bình Hành
Công thức tính chu vi của hình thoi

Muốn tính chu vi hình thoi ta lấy tổng độ dài của các cạnh hoặc độ dài một cạnh nhân với 4. Công thức tính chu vi hình thoi như sau:
P= a + a + a + a = a x 4
Trong đó: P là chu vi hình thoi
a là chiều dài của cạnh hình thoi
Ví dụ: Cho một hình thoi ABCD có độ dài các cạnh bằng nhau và bằng 4 cm. Hỏi chu vi của hình thoi bằng bao nhiêu?
Áp dụng công thức tính chu vi hình thoi, có cạnh a=4cm
Giải: Chu vi của hình thoi ABCD là:
4 x 4 = 16(cm)
Đáp số: 16 cm
Công thức tính diện tích của hình thoi

Diện tích hình thoi bằng một nửa tích độ dài của hai đường chéo, đường chéo của hình thoi là đường thẳng nối các đỉnh đối diện với nhau( hai đường chéo của hình thoi sẽ vuông góc với nhau và cắt nhau tại một điểm). Ta có công thức tính diện tích hình thoi như sau:
S = 1/2 x (d1 x d2)
Trong đó:
S là diện tích hình thoi
d1 là đường chéo d1
d2 là đường chéo d2
Ví dụ: Cho hình thoi ABCD có độ dài hai đường chéo lần lượt là 6cm và 10cm. Tính diên tích hình thoi ABCD?
Giải:
Diện tích của hình thoi ABCD là:
6 x 10 : 2 = 30 (cm2 )
Đáp số: 30 (cm2 )
Ngoài công thức trên ta còn có một số cách khác để tính diện tích hình thoi như sau
Thứ nhất, công thức tính diện tích hình thoi dựa trên hệ thức trong tam giác( trong trường hợp biết được số đo góc của hình thoi
S = a^2. sinA = a^2 . sinB = a^2.sinC = a^2. sinD
Ví dụ: Cho hình thoi ABCD có cạnh hình thoi là 4 cm và góc A có số đo là . Tính diện tích của hình thoi ABCD?
Cách 1:
Diện tích của hình thoi ABCD là:
S = a^2. sinA = 4^2 .sin〖30〗^0 = 16 . 1/2 = 8 (〖cm〗^2)
Vậy diện tích hình của hình thoi ABCD là 8 〖cm〗^2
Cách 2:
Vì ABCD là hình thoi nên các tam giác tạo thành là tam giác cân
Gọi O là giao điểm của hai đường chéo AC, BD và O cũng là trung điểm của hai đường chéo này nên AO vuông góc với BD. Do đó góc BAO = . 1/2 góc BAD = 〖15〗^0
Nên AO = AB = AB. Cos BAO = 4 . cos〖15〗^0 = 3,84 (cm)
Áp dụng định lý Py-ta-go vào tam giác AOB ta được:
〖AB〗^2= 〖AO〗^2 + 〖OB〗^2 => 〖OB〗^2= 〖AB〗^2- 〖AO〗^2 = 4^2 – 〖3,84〗^2 = 1,25
OB = 1,1(cm)
Từ đó : AC = 3. AO = 2. 3,84 = 7,68 (cm) và BD = 2. OB = 2. 1,1 = 2,2(cm)
Diện tích của hình thoi ABCD là 8,45 〖cm〗^2
Vậy diện tích của hình thoi ABCD là 8,45 〖cm〗^2
Thứ 2, công thức tính diện tích hình thoi dựa vào cạnh đáy và chiều cao
S= h x a
Trong đó:
S là diện tích hình thoi
h là chiều cao của hình thoi
a là cạnh đáy
Ví dụ: Cho hình thoi ABCD có cạnh AB = BC = CD = DA = 5(cm), chiều cao của hình thoi bằng 4 cm. Tính diện tích của hình thoi
Giải:
Áp dụng công thức tính diện tích hình thoi ta có:
h = 4(cm), a = 5(cm) ta được:
S= a x h = 5 x 4 = 20 (〖cm〗^2)
Vậy diện tích của hình thoi ABCD là 20 (〖cm〗^2)
Xem thêm>>[Toán Học] Hình Nón. Diện Tích Xung Quanh Hình Nón
Một số ví dụ áp dụng công thức tính chu vi và tính diện tính của hình thoi
Ví dụ 1: Một khu đất hình thoi có tổng độ dài hai đường chéo là 400 cm biết độ dài đường chéo thứ nhất bằng 3/5 độ dài đường chéo thứ hai. Tính diện tích khu đất hình thoi đó?
Giải:
Tổng số phần bằng nhau là: 3 + 5 = 8 ( phần)
Độ dài đường chéo thứ hai là: 400 : 8 x 5 = 250 (cm)
Độ dài đường chéo thứ nhất: 400 – 250 = 150(cm)
Diện tích của hình thoi là: 250 x 150 : 2 = 18750 (〖cm〗^2)
Đáp số : 18750 (〖cm〗^2)
Ví dụ 2: Một khu đất hình thoi có độ dài đường chéo thứ nhất là 20m, đường chéo thứ hai có độ dài bằng 3/4 độ dài đường chéo thứ nhất. Bác nông dân có trồng khoai tây trên khu đất này và được biết mỗi mét vuông đất thì thu hoạch được 5kg. Hỏi bác nông dân thu hoạch được bao nhiêu li-lo-gam khoai tây?
Giải:
Độ dài đường chéo thứ hai là: 20 : 4 x 3 = 15(m)
Diện tích khu đất hình thoi là: 20 x 15 : 2 = 150 (m^2)
Số khoai tây thu hoạch được trên khu đất là: 150 x 5 = 750( kg)
Đáp số: 750 kg khoai tây
Ví dụ 3: Cho hình thoi ABCD có O là giao điểm của hai đường chéo được biết diện tích hình thoi là 60 〖cm〗^2 và AC = 10cm. Tính độ dài cạnh của hình thoi?
Giải:
Diện tích của hình thoi là:
S = ½. AC. BD => BD = (2.S)/AC = (2.60)/10 = 12(cm)
Theo tính chất của hình thoi ta có: O là trung điểm của AC và BD nên
OA = ½ . AC = ½ . 10 = 5(cm) và OB = ½ . BD = ½ . 12= 6(cm)
Áp dụng định lý Py-ta-go vào tam giác AOB ta có:
〖AB〗^2= 〖AO〗^2 + 〖OB〗^2 = 5^2+ 6^2 = 61 => AB = 7,81(cm)
Vậy độ dài cạnh của hình thoi là 7,81 cm
Xem ngay>> [Toán học] Công Thức Cách Tính Chiều Dài Chiều Rộng Hình Chữ Nhật Và Ví Dụ Có Lời Giải
Trên đây là bìa viết tham khảo của thuthuatpc.vn về công thức tính chu vi và diện tích hình thoi bài viết đăng tải nhằm mục đích giáo dục, không nhằm mục đích thương mại. Hy vọng đã cung cấp cho bạn đọc những thông tin hữu ích. Cảm ơn các bạn đã theo dõi bài viết của mình.
